การประยุกต์สไปลน์กำลังสามเพื่อประมาณค่าอินทิกรัลจำกัดเขต
Main Article Content
บทคัดย่อ
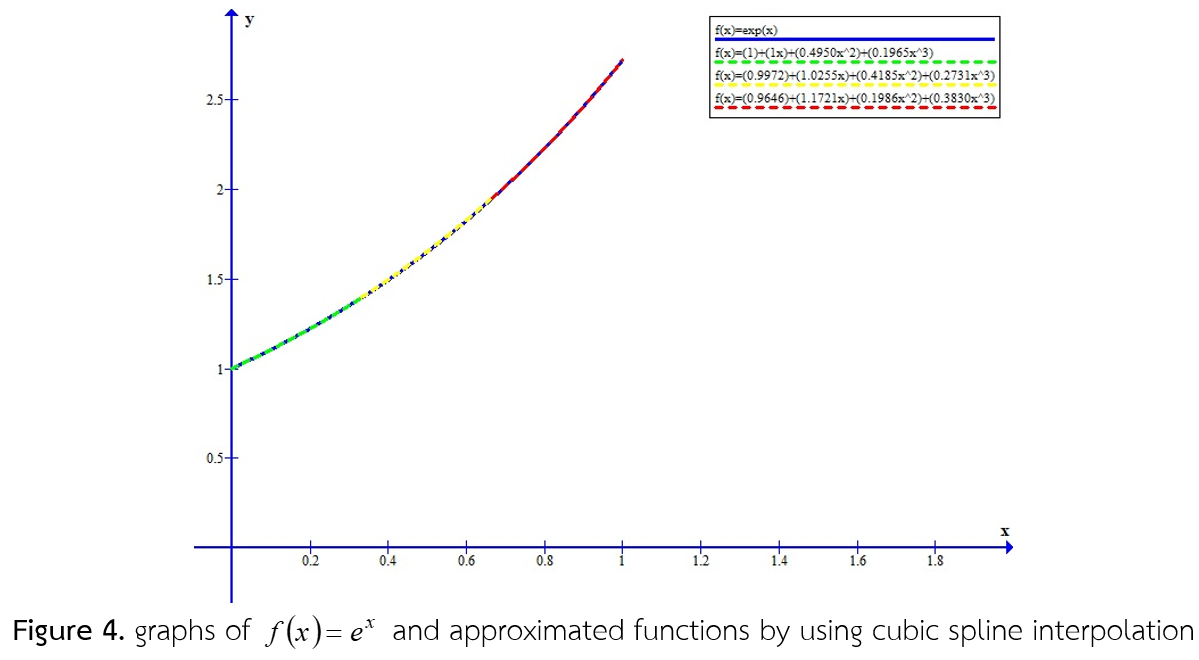
การประมาณค่าอินทิกรัลจำกัดเขตเป็นเรื่องที่นักคณิตศาสตร์ให้ความสนใจศึกษาเรื่องหนึ่ง โดยเฉพาะอย่างยิ่งสำหรับฟังก์ชันที่หาค่าอินทิกรัลเชิงวิเคราะห์ไม่ได้ ซึ่งมีการเสนอหลายวิธีเพื่อใช้ในการหาประมาณค่าอินทิกรัลจำกัดเขต วิธีการประมาณอินทิกรัลจำกัดเขตวิธีการหนึ่งที่ให้ผลลัพธ์เป็นที่น่าพอใจ คือ การประมาณฟังก์ชันที่อินทิกรัลเชิงวิเคราะห์ไม่ได้ด้วยฟังก์ชันที่อินทิกรัลเชิงวิเคราะห์ได้ ถ้าฟังก์ชันประมาณเป็นฟังก์ชันที่ดีที่สามารถแทนฟังก์ชันที่ต้องการพิจารณาอินทิกรัลจำกัดเขต แล้วอินทิกรัลจำกัดเขตของฟังก์ชันประมาณก็จะเป็นค่าประมาณที่ดีที่สามารถแทนอินทิกรัลจำกัดเขตของฟังก์ชันที่ต้องการพิจารณาได้ สำหรับบทความนี้มีจุดประสงค์เพื่อศึกษาการประมาณฟังก์ชันด้วยการประมาณค่าในช่วงโดยใช้สไปลน์กำลังสาม และเพื่อประยุกต์ฟังก์ชันประมาณที่ได้จากการประมาณค่าในช่วงโดยใช้สไปลน์กำลังสาม เพื่อประมาณอินทิกรัลจำกัดเขตของฟังก์ชัน ในบทความได้นำเสนอการประมาณฟังก์ด้วยการประมาณค่าในช่วงโดยใช้สไปลน์กำลัง ทั้งฟังก์ชันที่หาค่าอินทิกรัลเชิงวิเคราะห์ได้และหาค่าอินทิกรัลเชิงวิเคราะห์ไม่ได้ เพื่อให้เห็นชัดเจนถึงวิธีการประยุกต์สไปลน์กำลังสามเพื่อประมาณค่าอินทิกรัลจำกัดเขต
Article Details
วารสารวิทยาศาสตร์และวิทยาศาสตร์ศึกษา (JSSE) เป็นผู้ถือลิสิทธิ์บทความทุกบทความที่เผยแพร่ใน JSSE นี้ ทั้งนี้ ผู้เขียนจะต้องส่งแบบโอนลิขสิทธิ์บทความฉบับที่มีรายมือชื่อของผู้เขียนหลักหรือผู้ที่ได้รับมอบอำนาจแทนผู้เขียนทุกนให้กับ JSSE ก่อนที่บทความจะมีการเผยแพร่ผ่านเว็บไซต์ของวารสาร
แบบโอนลิขสิทธิ์บทความ (Copyright Transfer Form)
ทางวารสาร JSSE ได้กำหนดให้มีการกรอกแบบโอนลิขสิทธิ์บทความให้ครบถ้วนและส่งมายังกองบรรณาธิการในข้อมูลเสริม (supplementary data) พร้อมกับนิพนธ์ต้นฉบับ (manuscript) ที่ส่งมาขอรับการตีพิมพ์ ทั้งนี้ ผู้เขียนหลัก (corresponding authors) หรือผู้รับมอบอำนาจ (ในฐานะตัวแทนของผู้เขียนทุกคน) สามารถดำเนินการโอนลิขสิทธิ์บทความแทนผู้เขียนทั้งหมดได้ ซึ่งสามารถอัพโหลดไฟล์บทความต้นฉบับ (Manuscript) และไฟล์แบบโอนลิขสิทธิ์บทความ (Copyright Transfer Form) ในเมนู “Upload Submission” ดังนี้
1. อัพโหลดไฟล์บทความต้นฉบับ (Manuscript) ในเมนูย่อย Article Component > Article Text
2. อัพโหลดไฟล์แบบโอนลิขสิทธิ์บทความ (Copyright Transfer Form) ในเมนูย่อย Article Component > Other
ดาวน์โหลด ไฟล์แบบโอนลิขสิทธิ์บทความ (Copyright Transfer Form)
เอกสารอ้างอิง
Bittinger, M. L., Ellenbogen, D. J. and Surgent, S. J. (2015). Calculus and its applications (10th ed.). Boston, MA: Pearson Education.
Burden, R. L. and Faires, J. D. (2001). Numerical Analysis (7th ed.). Stamford, CT: Thomson Learning.
Burt, P. J. and Adelson, E. H. (1983). A multiresolution spline with application to image mosaics. ACM transactions on Graphics, 2(4), 217-236.
Eldén, L. and Wittmeyer-Koch, L. (1990). Numerical Analysis: An Introduction. Boston, MA: Academic Press.
Giordano, F. R., Fox, W. P. and Horton, S. B. (2013). A First Course in Mathematical Modeling (5th ed.). Ontario: Nelson Education.
Heinbockel, J. H. (2012). Introduction to Calculus. Old Dominion University. Retrieved 6 Nov 2019, from http://www.math.odu.edu/~jhh/counter10.html
Kastanek, F. J. and Nielsen, D. R. (2001). Description of soil water characteristics using cubic spline interpolation. Soil Science Society of America Journal, 65(2), 279-283.
Kawamura, H., Sasaki, T. and Otsuki, T. (1992). Spline interpolation method. U.S. Patent No. 5,140,236. Washington, DC: U.S. Patent and Trademark Office.
McKinley, S. and Levine, M. (1998). Cubic spline interpolation. College of the Redwoods, 45(1), 1049-1060.
Scardapane, S., Scarpiniti, M., Comminiello, D. and Uncini, A. (2017, June). Learning activation functions from data using cubic spline interpolation. In Italian Workshop on Neural Networks (pp. 73-83). Retrieved 6 Nov 2019, from https://arxiv.org/pdf/1605.05509.pdf
Steven, C. C. (2007). Applied Numerical Methods with Matlab for Engineers and Scientists. New York: McGraw-Hill Higher Education
Wang, Y., Shen, D. and Teoh, E. K. (2000). Lane detection using spline model. Pattern Recognition Letters, 21(8), 677-689.