การสร้างตัวแบบเชิงคณิตศาสตร์เกี่ยวกับสถานะตลาดหุ้น โดยใช้ระบบ สมการเชิงผลต่าง

บทคัดย่อ

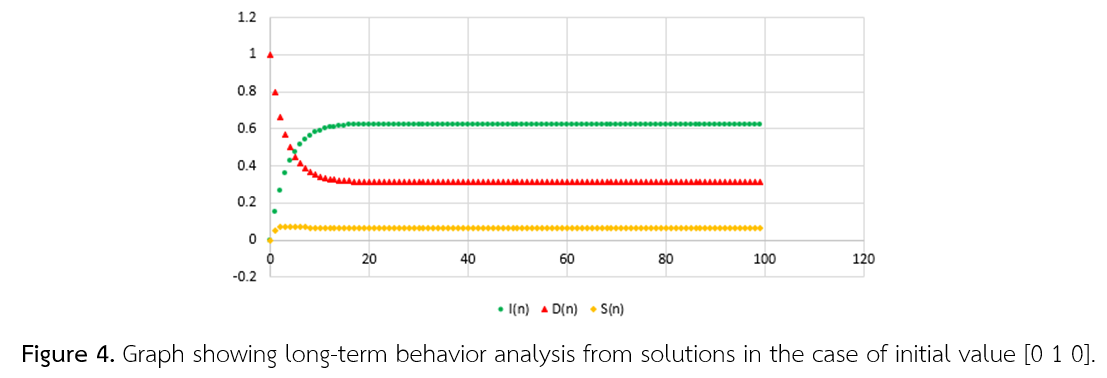
การวิจัยครั้งนี้มีวัตถุประสงค์เพื่อนำเสนอการสร้างตัวแบบเชิงคณิตศาสตร์ของสถานะตลาดหุ้นโดยใช้ระบบสมการเชิงผลต่าง เริ่มต้นด้วยการศึกษารูปแบบการวิเคราะห์ในรูปลูกโซ่มาร์คอฟแล้วแปลงเป็นระบบสมการเชิงผลต่าง ซึ่งสามารถพิจารณาผลเฉลยเชิงวิเคราะห์ แตกต่างจากการหาผลเฉลยตัวแบบที่อยู่ในรูปลูกโซ่มาร์คอฟ ที่ต้องอาศัยวิธีการเชิงตัวเลข เพื่อหาผลเฉลยเชิงตัวเลข ในขั้นตอนการพิจารณาผลเฉลยของระบบสมการเชิงผลต่างนั้น มีการใช้โปรแกรมวูลแฟรมแอลฟา เพื่อช่วยหาสมการลักษณะเฉพาะ ค่าเจาะจง และค่าเวกเตอร์เจาะจง และมีการใช้โปรแกรมไมโครซอฟท์เอกซ์เซล ในการหาผลเฉลยเชิงตัวเลข และการแสดงกราฟของผลเฉลย สำหรับตัวแบบเชิงคณิตศาสตร์เกี่ยวกับสถานะหุ้นนั้น มีการพิจารณาสถานะเป็น ตลาดขาขึ้น ตลาดขาลง และตลาดหยุดนิ่ง การวิเคราะห์สถานะเพื่อให้เห็นพฤติกรรมระยะยาว กรณีหุ้นที่นำมาศึกษานี้ มีการพิจารณาค่าเริ่มต้นของสถานะ 3 กรณี คือ  [1 0 0] , [0 1 0] และ [0 0 1] ซึ่งผลการศึกษาพบว่าพฤติกรรมระยะยาวของสถานะหุ้นที่มีค่าเริ่มต้นทั้ง 3 กรณีได้ผลลัพธ์เหมือนกัน คือ มีความน่าจะเป็นของสถานะตลาดขาขึ้นเป็น 0.6250 ตลาดขาลงเป็น 0.3125  และตลาดหยุดนิ่ง 0.0625 ชี้ให้เห็นว่าเมื่อเวลาผ่านไปหุ้นที่นำมาศึกษามีความน่าจะเป็นที่จะเป็นตลาดขาขึ้น ซึ่งจะเป็นข้อมูลสารสนเทศเชิงคณิตศาสตร์ที่มีประโยชน์ข้อมูลหนึ่งเพื่อใช้พิจารณาร่วมกับข้อมูลด้านอื่นในการซื้อขาย