การเข้ารหัสและถอดรหัสโดยการใช้เมทริกซ์เพลล์และเพลล์ที่ปรับปรุงแล้ว
Main Article Content
บทคัดย่อ
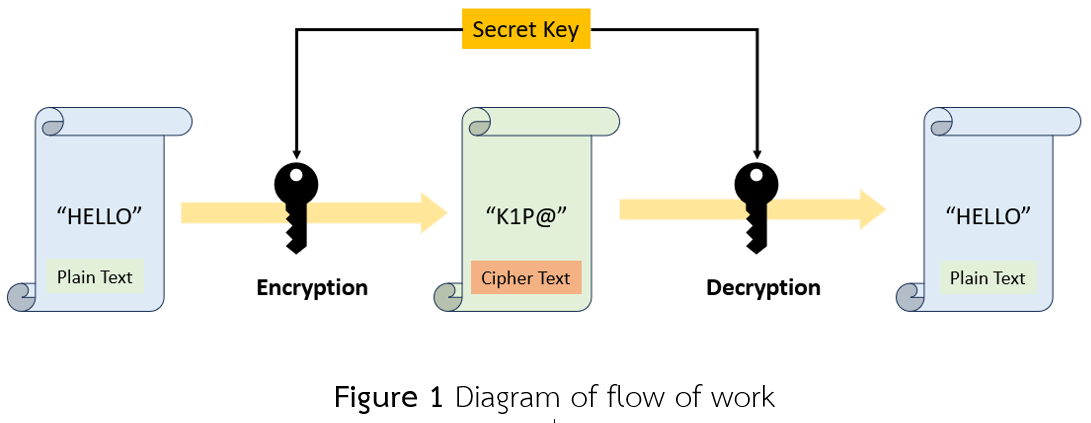
บทความวิจัยนี้ คณะผู้วิจัยได้ศึกษาเมทริกซ์เพลล์และเพลล์ที่ปรับปรุงเเล้วที่สมาชิกในเมทริกซ์เกี่ยวข้องกับลำดับเพลล์และลำดับเพลล์ที่ปรับปรุงแล้ว นอกจากนี้ คณะผู้วิจัยได้นำเมทริกซ์ดังกล่าวมาใช้ในการนำเสนอขั้นตอนวิธีการใหม่สำหรับการเข้ารหัสซึ่งแปลงข้อความธรรมดาเป็นข้อความที่ได้รับการเข้ารหัสเพื่อความปลอดภัยในการส่งข้อมูลและการถอดรหัสเป็นขั้นตอนในการแปลรหัสข้อความที่ได้รับการเข้ารหัสเพื่อให้ได้ข้อความเดิม
Article Details

อนุญาตภายใต้เงื่อนไข Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
วารสารวิทยาศาสตร์และวิทยาศาสตร์ศึกษา (JSSE) เป็นผู้ถือลิสิทธิ์บทความทุกบทความที่เผยแพร่ใน JSSE นี้ ทั้งนี้ ผู้เขียนจะต้องส่งแบบโอนลิขสิทธิ์บทความฉบับที่มีรายมือชื่อของผู้เขียนหลักหรือผู้ที่ได้รับมอบอำนาจแทนผู้เขียนทุกนให้กับ JSSE ก่อนที่บทความจะมีการเผยแพร่ผ่านเว็บไซต์ของวารสาร
แบบโอนลิขสิทธิ์บทความ (Copyright Transfer Form)
ทางวารสาร JSSE ได้กำหนดให้มีการกรอกแบบโอนลิขสิทธิ์บทความให้ครบถ้วนและส่งมายังกองบรรณาธิการในข้อมูลเสริม (supplementary data) พร้อมกับนิพนธ์ต้นฉบับ (manuscript) ที่ส่งมาขอรับการตีพิมพ์ ทั้งนี้ ผู้เขียนหลัก (corresponding authors) หรือผู้รับมอบอำนาจ (ในฐานะตัวแทนของผู้เขียนทุกคน) สามารถดำเนินการโอนลิขสิทธิ์บทความแทนผู้เขียนทั้งหมดได้ ซึ่งสามารถอัพโหลดไฟล์บทความต้นฉบับ (Manuscript) และไฟล์แบบโอนลิขสิทธิ์บทความ (Copyright Transfer Form) ในเมนู “Upload Submission” ดังนี้
1. อัพโหลดไฟล์บทความต้นฉบับ (Manuscript) ในเมนูย่อย Article Component > Article Text
2. อัพโหลดไฟล์แบบโอนลิขสิทธิ์บทความ (Copyright Transfer Form) ในเมนูย่อย Article Component > Other
ดาวน์โหลด ไฟล์แบบโอนลิขสิทธิ์บทความ (Copyright Transfer Form)
เอกสารอ้างอิง
Ercolano, J. (1979). Matrix generators of Pell sequences. Fibonacci Quart, 17(1), 71-77.
Flaut, C. (2019). Some application of difference equations in Cryptography and Coding Theory. Journal of Difference Equations and Applications, 25(7), 905-920.
Halici, S. and Daşdemir, A. (2010). On some relationships among Pell, Pell-Lucas and modified Pell sequences. Sakarya University Journal of Science, 14(2), 141-145.
Hoggatt Jr, V. E. and Ruggles, I. D. (1963). A Primer for the Fibonacci Numbers-Part IV. The Fibonacci Quarterly, 1(4), 39-45.
Horadam, A. F. (1994). Applications of modified Pell numbers to representations. Ulam Quarterly, 3(1),34-53.
Shtayat, J. and Al-Kateeb, A. (2019). An Encoding-Decoding algorithm based on Padovan numbers. arXiv preprint arXiv, 1907.02007.
Shtayat, J. and Al-Kateeb, A. (2022). The Perrin -matrix and more properties with an application. Journal of Discrete Mathematical Sciences and Cryptography, 25(1), 41-52.
Stakhov, A. P. (1999). A generalization of the Fibonacci -matrix. Reports of the National Academy of Sciences of Ukraine, 9, 46-49.
Sundarayya, P. and Vara Prasad, G. (2019). A public key cryptosystem using Affine Hill Cipher under modulation of prime number. Journal of Information and Optimization Sciences, 40(4), 919-930.
Sümeyra, U. Ç. A. R., Nihal, T. A. Ş. and Özgür, N. Y. (2019). A new application to coding theory via Fibonacci and Lucas numbers. Mathematical Sciences and Applications E-Notes, 7(1), 62-70.
Taş, N., Uçar, S., Özgür, N. Y. and Kaymak, Ö. Ö. (2018). A new coding/decoding algorithm using Fibonacci numbers. Discrete Mathematics, Algorithms and Applications, 10(02), 1850028.