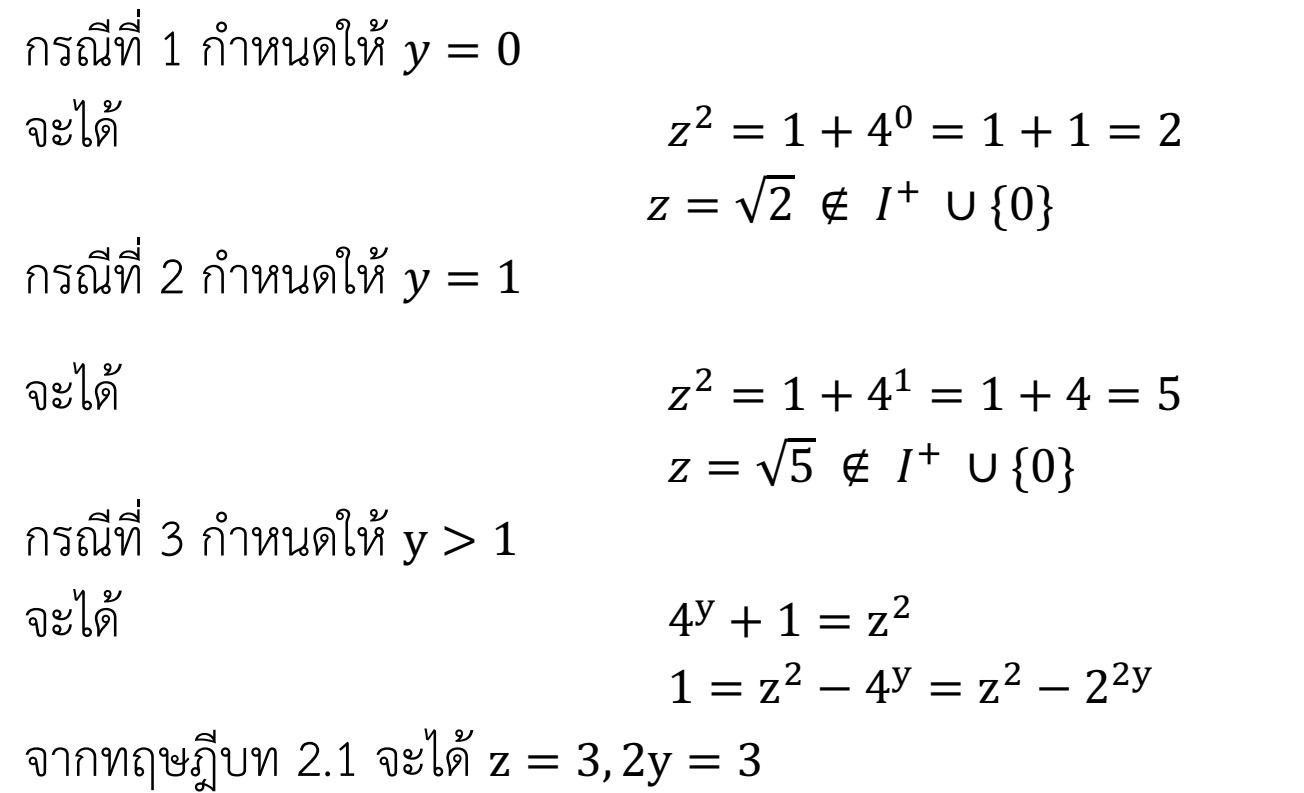The solution of the diophantine equation forms 24^x+4^y=z^2 and 35^x+4^y=z^2

Article Sidebar

PDF
Published: Jan 2, 2023
Keywords:
Diophantine equation, Non-negative integer, Solutions 24x 4y = z2 and 35x 4y = z2

Main Article Content

Patchara Muangkarn
Mathematics program Faculty of Science and Technology Kamphaeng Phet Rajabhat University
Sutipong Khamtheang
Mathematics program Faculty of Science and Technology Kamphaeng Phet Rajabhat University
Cholatis Suanoom
Mathematics program Faculty of Science and Technology Kamphaeng Phet Rajabhat University

Abstract

In this paper, we find positive integral solutions of the Diophantine equation gif.latex?24^x+4^y=z^2 and gif.latex?35^x+4^y=z^2 Moreover, we proved the Diophantine equation. by creating mathematical tools.

Article Details

Issue
Vol. 2 No. 2 (2022): July-December (2022)
Section
Research articles

References

Acu, D., 2007. On a Diophantine Equation 2x +

David, M. B., 2007. Elementary Number Theor

Kenneth, H. R., 2000. Elementary Number Th

Wesley Longman, Inc.

Mordell, L. J. 1969. Diophantine Equations. Ac

Sandor, J. 2002. On a diophantine equation 3x

equations and arithmetic functions. Amer

[ 6 ] Sandor, J. 2 0 0 2 . On a Diophantine equat

Diophantine equations and arithmetic fun

, 91-92.

Sierpinski, W. 1964. Elementary Theory of Num

Silverman, J. H. 2001. A Friendly Introduction

Inc., New Jersey,

Suvarnamani,A. 2011. Solution of the Diophantine

Sciences and Applications, 1(3), Septemb

Mihailescu, P. 2004. Primary cycolotomic u

Reine Angew. Math. 27, 167-195

Suvarnamani, A. & Singtaand,A. & Chotchaisthit

x + 7y = z2and 4x + 11y = z2, Science a

[ 12] sammsa, A. 2020. Diophantine equations

Rajabhat Mathematics Journal, 67 – 71.