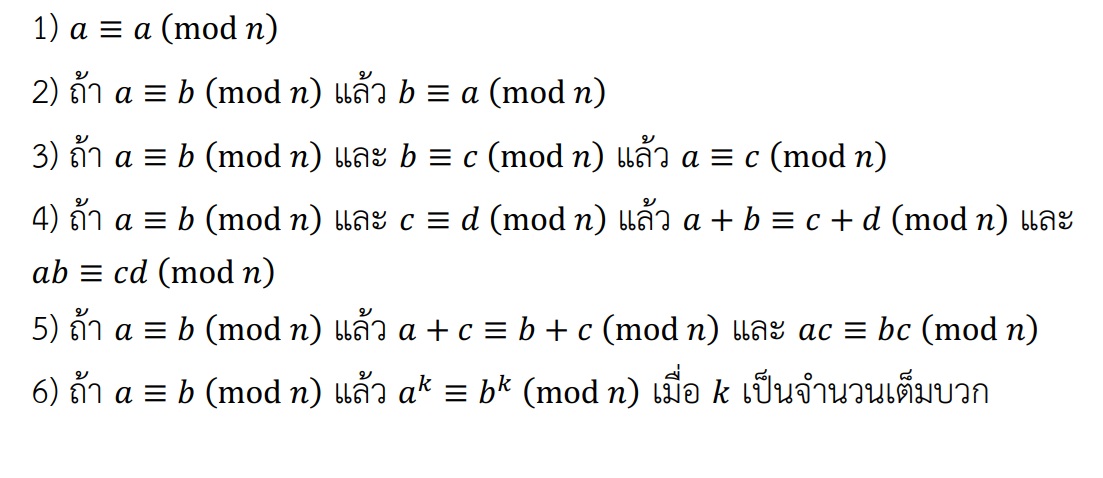The solutions of the Diophantine equations 〖11〗^x-3^y=z^2 and 〖14〗^x-3^y=z^2
Main Article Content
Abstract
In this paper, we study all solutions of the Diophantine equations and
, where
and
are non-negative integers. By using the elementary concepts of congruence and Mihăilescu’s Theorem, we show that the Diophantine equation
has the unique non-negative integer solution
, which is
. The Diophantine equation
has exactly two non-negative integer solutions
, which are
and
.
Article Details
References
Burshtein, N. 2020. All the solutions of the Diophantine equations 〖13〗^x-5^y=z^2 ,〖19〗^x-5^y=z^2 in positive integers x,y,z. Annals of Pure and Applied Mathematics, 22(2): 93-96.
Burton, D.M. 2010. Elementary number theory. 7th ed., New York: McGraw-Hill.
Chuayjan, W., Thongnak, S. and Kaewong, T. 2023. On the exponential Diophantine equation 3^x-5^y=z^2. Annals of Pure and Applied Mathematics, 28(1): 25-28.
Gope, R.C. 2023. On the exponential Diophantine equation 〖27〗^x-〖11〗^y=z^2 . Journal of Physical Sciences, 28: 11-15.
Kaewong, T., Chuayjan, W. and Thongnak, S. 2023. On the exponential Diophantine equation 〖29〗^x-3^y=z^2. International Journal of Latest Technology in Engineering, Management & Applied Science, 12(11): 74-76.
Mihăilescu, P. 2004. Primary cyclotomic units and a proof of Catalan’s conjecture. Journal für die Reine und Angewandte Mathematik, 572: 167-195.
Rao, C.G. 2022. On the exponential Diophantine equation 〖23〗^x-〖19〗^y=z^2 . Journal of Physical Sciences, 27: 1-4.
Siraworakun, A. and Tadee, S. 2024. All solutions of the Diophantine equation 〖25〗^x-7^y=z^2. International Journal of Mathematics and Computer Science, 19(3): 631-633.
Tadee, S. 2023. A short note on two Diophantine equations 9^x-3^y=z^2 and 〖13〗^x-7^y=z^2. Journal of Mathematics and Informatics, 24: 23-25.
Thongnak, S., Chuayjan, W. and Kaewong, T. 2019. On the exponential Diophantine equation 2^x-3^y=z^2. Southeast-Asian Journal of Sciences, 7(1): 1-4.
Thongnak, S., Chuayjan, W. and Kaewong, T. 2021. The solution of the exponential Diophantine equation 7^x-5^y=z^2. Mathematical Journal by The Mathematical Association of Thailand under the Patronage of His Majesty the King, 66(703): 62-67.
Thongnak, S., Chuayjan, W. and Kaewong, T. 2022. On the Diophantine equation 7^x-2^y=z^2 where x,y and z are non-negative integers. Annals of Pure and Applied Mathematics, 25(2): 63-66.
Thongnak, S., Kaewong, T. and Chuayjan, W. 2024. On the exponential Diophantine equation 5^x-3^y=z^2. International Journal of Mathematics and Computer Science, 19(1): 99-102.