การเปรียบเทียบเชิงประจักษ์ของอัลกอริธึมการหารากระหว่างวิธีดั้งเดิมและวิธีผสม
Main Article Content
บทคัดย่อ
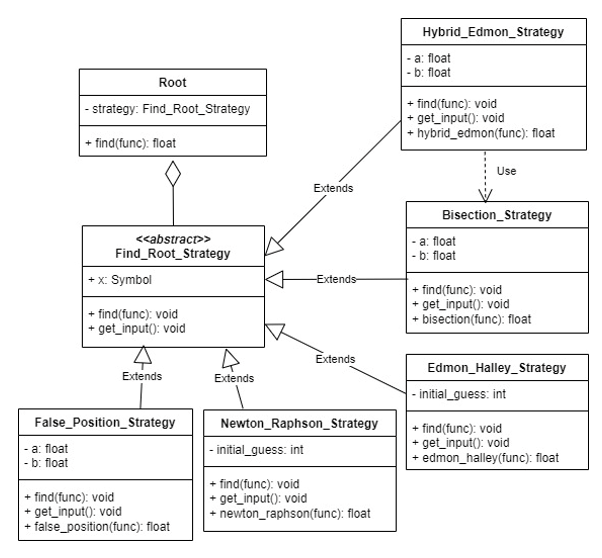
การวิจัยนี้นำเสนอวิธีการใหม่ที่พัฒนาขึ้นจากการผสมผสานเทคนิคดั้งเดิม ได้แก่ วิธีแบ่งครึ่งช่วง วิธีแก้ตำแหน่งผิด และวิธีของเอ็ดมอนด์-ฮัลเลย์ เพื่อเพิ่มประสิทธิภาพของอัลกอริธึมในการหาค่าราก การวิจัยยังเปรียบเทียบประสิทธิภาพของวิธีการแบบดั้งเดิมเหล่านี้กับวิธีผสมใหม่โดยการเขียนโค้ดในภาษาไพธอน ผลการวิจัยแสดงให้เห็นว่าวิธีการใหม่มีประสิทธิภาพสูงกว่า วิธีการแบบดั้งเดิม นอกจากนี้ ยังได้พัฒนาโครงสร้างของคลาสที่อิงกับการออกแบบแบบรูปกลยุทธ เพื่อการนำโค้ดไปใช้ที่อย่างเป็นระบบ เพื่อช่วยเพิ่มความสามารถในการบำรุงรักษาและการขยายตัวของอัลกอริธึม
Article Details

อนุญาตภายใต้เงื่อนไข Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
วารสารวิทยาศาสตร์และวิทยาศาสตร์ศึกษา (JSSE) เป็นผู้ถือลิสิทธิ์บทความทุกบทความที่เผยแพร่ใน JSSE นี้ ทั้งนี้ ผู้เขียนจะต้องส่งแบบโอนลิขสิทธิ์บทความฉบับที่มีรายมือชื่อของผู้เขียนหลักหรือผู้ที่ได้รับมอบอำนาจแทนผู้เขียนทุกนให้กับ JSSE ก่อนที่บทความจะมีการเผยแพร่ผ่านเว็บไซต์ของวารสาร
แบบโอนลิขสิทธิ์บทความ (Copyright Transfer Form)
ทางวารสาร JSSE ได้กำหนดให้มีการกรอกแบบโอนลิขสิทธิ์บทความให้ครบถ้วนและส่งมายังกองบรรณาธิการในข้อมูลเสริม (supplementary data) พร้อมกับนิพนธ์ต้นฉบับ (manuscript) ที่ส่งมาขอรับการตีพิมพ์ ทั้งนี้ ผู้เขียนหลัก (corresponding authors) หรือผู้รับมอบอำนาจ (ในฐานะตัวแทนของผู้เขียนทุกคน) สามารถดำเนินการโอนลิขสิทธิ์บทความแทนผู้เขียนทั้งหมดได้ ซึ่งสามารถอัพโหลดไฟล์บทความต้นฉบับ (Manuscript) และไฟล์แบบโอนลิขสิทธิ์บทความ (Copyright Transfer Form) ในเมนู “Upload Submission” ดังนี้
1. อัพโหลดไฟล์บทความต้นฉบับ (Manuscript) ในเมนูย่อย Article Component > Article Text
2. อัพโหลดไฟล์แบบโอนลิขสิทธิ์บทความ (Copyright Transfer Form) ในเมนูย่อย Article Component > Other
ดาวน์โหลด ไฟล์แบบโอนลิขสิทธิ์บทความ (Copyright Transfer Form)
เอกสารอ้างอิง
Bogdanov, V. V. and Volkov, Y. S. (2013). A modified quadratic interpolation method for root finding. Journal of Applied and Industrial Mathematics, 17(3), 491-497.
Burden, R. L. and Faires, J. D. (2001). Numerical Analysis. USA: Brooks/Cole.
Cortez, M. V., Ali, N. Z., Khan, A. G. and Awan M. U. (2023). Numerical analysis of new hybrid algorithms for solving nonlinear equations. Axioms, 12(7), 684.
Gemechu, T. and Thota, S. (2020). On new root finding algorithms for solving nonlinear transcendental equations. International Journal of Chemistry Mathematics and Physics, 4(2), 18-24.
Gamma, E., Helm, R., Johnson, R. and Vlissides J. (1994). Design Patterns: Elements of Reusable Object-Oriented Software. Addison-Wesley. Indianapolis: Addison-Wesley.
Jun, Y. and Jeon, J. (2019). Modified bisection method for solving nonlinear equations. International Journal of Scientific and Innovation Mathematical Research, 7(9), 8-11.
Khairin, A., Kusumo, D. and Priyadi, Y. (2022). Analysis of The Impact of Software Detailed Design on Mobile Application Performance Metrics. Building of Informatics. Technology and Science (BITS), 4(1), 226−234.
Kincaid, D. and Cheney, W. (1990). Numerical analysis mathematics of scientific computing. USA: Brook/Cole.
Ngaogate, W., Jean, A., Wattanataweekul, R., Janngam, K. and Alherbe, T. (2024). Hybrid Machine Learning Algorithm with Fixed Point Technique for Medical Data Classification Problems Incorporating Data Cryptography. Thai Journal of Mathematics, 22(2), 295–310.
Noor, K. I. and Noor, M. A. (2007). Predictor-Corrector Halley method for nonlinear equations. Applied Mathematics and Computation, 188, 1587-1591.
Qamar, N and Malik, A. A. (2020). Impact of Design Patterns on Software Complexity and Size. Mehran University Research Journal of Engineering and Technology, 39(2), 342-352.
Sabharwai, C. L. (2019). Blended root finding algorithm outperforms bisection and regula falsi algorithm. Mathematics, 7(11), 1-16.
Sarcar, V. (2022). Java Design Patterns: A Hands-On Experience with Real-World Examples (Third Edition). USA: Apress.
Tanakan, S. (2013). A new algorithm of modified bisection method for nonlinear equation. Applied Mathematical Sciences, 7(123), 16107-16114.