ความน่าจะเป็นของคุณสมบัติย้อนกลับบนกรุปการหมุนรูป
Article Sidebar
Main Article Content
บทคัดย่อ
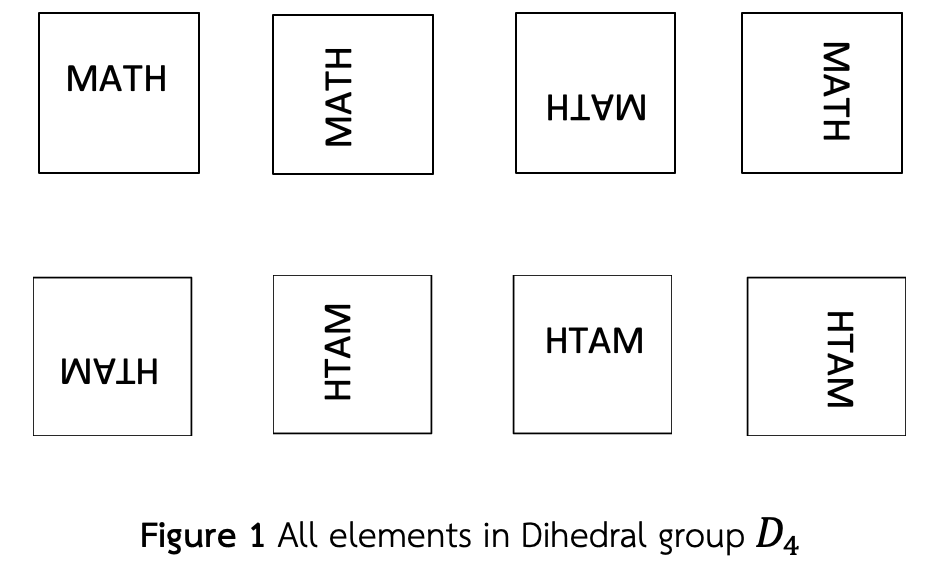
เป็นที่ทราบกันดีว่า คุณสมบัติหนึ่งที่สำคัญของกรุปคือ คุณสมบัติการสลับที่ เราสนใจว่ากรุปไม่สลับที่บางกรุปนั้น ห่างไกลจากคุณสมบัติการสลับที่เพียงใด Gallian (2010) ได้อธิบายวิธีที่จะวัดค่าการสลับที่ของกรุปจำกัด โดยใช้แนวคิดของความน่าจะเป็น และกำหนดให้ แทนความน่าจะเป็นที่สองสมาชิกที่ถูกเลือกมาแบบสุ่มนั้นสลับที่ได้ในกรุปจำกัด ต่อมา Clifton, Guichard และ Keef (2011) ได้ศึกษาความน่าจะเป็นดังกล่าวบนกรุปการหมุนรูป เมื่อ เป็นจำนวนเต็มบวก และพบรูปทั่วไปของ งานวิจัยของ Langley, Levitt และ Rower (2011) ขยายความคิดไปสู่ ซึ่งเป็นความน่าจะเป็นที่ผลคูณของสมาชิก ตัวในกรุปจำกัด มีคุณสมบัติย้อนกลับ งานวิจัยนี้ ศึกษาความน่าจะเป็นดังกล่าวและพบรูปทั่วไปของความน่าจะเป็นที่ผลคูณของสมาชิก ตัวในกรุปการหมุนรูปที่มีคุณสมบัติย้อนกลับ นั่นคือ
Downloads
Article Details
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
วารสารวิทยาศาสตร์และวิทยาศาสตร์ศึกษา (JSSE) เป็นผู้ถือลิสิทธิ์บทความทุกบทความที่เผยแพร่ใน JSSE นี้ ทั้งนี้ ผู้เขียนจะต้องส่งแบบโอนลิขสิทธิ์บทความฉบับที่มีรายมือชื่อของผู้เขียนหลักหรือผู้ที่ได้รับมอบอำนาจแทนผู้เขียนทุกนให้กับ JSSE ก่อนที่บทความจะมีการเผยแพร่ผ่านเว็บไซต์ของวารสาร
แบบโอนลิขสิทธิ์บทความ (Copyright Transfer Form)
ทางวารสาร JSSE ได้กำหนดให้มีการกรอกแบบโอนลิขสิทธิ์บทความให้ครบถ้วนและส่งมายังกองบรรณาธิการในข้อมูลเสริม (supplementary data) พร้อมกับนิพนธ์ต้นฉบับ (manuscript) ที่ส่งมาขอรับการตีพิมพ์ ทั้งนี้ ผู้เขียนหลัก (corresponding authors) หรือผู้รับมอบอำนาจ (ในฐานะตัวแทนของผู้เขียนทุกคน) สามารถดำเนินการโอนลิขสิทธิ์บทความแทนผู้เขียนทั้งหมดได้ ซึ่งสามารถอัพโหลดไฟล์บทความต้นฉบับ (Manuscript) และไฟล์แบบโอนลิขสิทธิ์บทความ (Copyright Transfer Form) ในเมนู “Upload Submission” ดังนี้
1. อัพโหลดไฟล์บทความต้นฉบับ (Manuscript) ในเมนูย่อย Article Component > Article Text
2. อัพโหลดไฟล์แบบโอนลิขสิทธิ์บทความ (Copyright Transfer Form) ในเมนูย่อย Article Component > Other
ดาวน์โหลด ไฟล์แบบโอนลิขสิทธิ์บทความ (Copyright Transfer Form)
The Journal of Science and Science Education (JSSE) retain the right of all articles published in JSSE. The coresponding author or the authorized person on behalf of the authors must send the complete Copyright Transfer Form to JSSE before any article get published in JSSE.
Copyright Transfer Form
The JSSE request the coresponding author or the authorized person on behalf of the authors upload the manuscript under the together with the Copyright Transfer Form under the supplementary data. The guidline for uploading both manuscript and Copyright Transfer Form is shown below:
1. Upload the manuscript in the sub-menu, Article Component > Article Text.
2. Upload the the Copyright Transfer Form in the sub-menu, Article Component > Other.
Download Copyright Transfer Form
References
Clifton, C., Guichard, D. and Keef, P. (2011). How commutative are direct products of Dihedral groups.
Mathematics Magazine, 84, 137-140.
Gallian, J. (2010). Contemporary Abstract Algebra (7th ed). Belmont, CA: Brooks Cole.
Langley, T., Levitt, D. and Rower, J. (2011). Two generalizations of 5/8 bound on commutativity in
nonabelian finite groups. Mathematics Magazine, 84, 128-136.
Nicholson, W. K., (2012). Introduction to Abstract Algebra (4th ed). New Jersey: Wiley.
Rotman, J. J. (1996). A first Course in Abstract Algebra. New Jersey: Prentice Hall.
Sherman, G.J. (1997). Trying to do group theory with undergraduates and computers. Journal of Symbolic
Computation.23, 577-587.