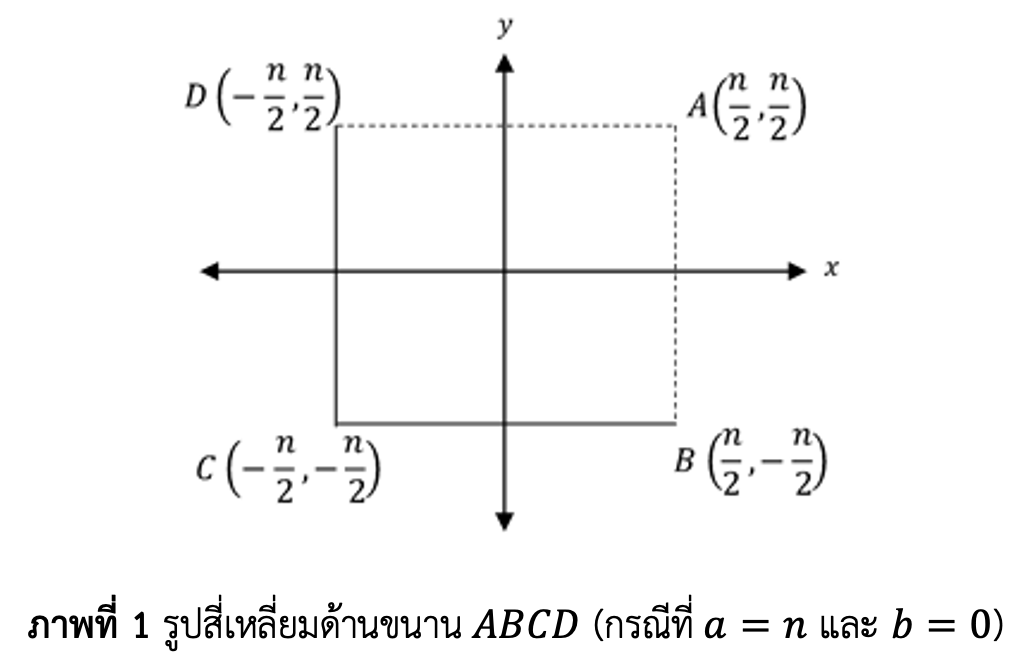
บางระบบส่วนตกค้างบริบูรณ์ในจำนวนเต็มเกาส์เซียน
Main Article Content
บทคัดย่อ
ในงานวิจัยนี้ได้ศึกษาบางระบบส่วนตกค้างบริบูรณ์ในจำนวนเต็มเกาส์เซียน โดยที่ระบบส่วนตกค้างบริบูรณ์ มอดุโล เมื่อ
เป็นจำนวนเต็มเกาส์เซียน ในที่นี้ จะเขียนย่อด้วย
ผลการวิจัยพบว่า สำหรับจำนวนเต็มบวก
1) เป็น
2) เป็น
3) เป็น
4) เป็น
5) เป็น
6) เป็น
7) เป็น
8) เป็น
Article Details

อนุญาตภายใต้เงื่อนไข Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
วารสารวิทยาศาสตร์และวิทยาศาสตร์ศึกษา (JSSE) เป็นผู้ถือลิสิทธิ์บทความทุกบทความที่เผยแพร่ใน JSSE นี้ ทั้งนี้ ผู้เขียนจะต้องส่งแบบโอนลิขสิทธิ์บทความฉบับที่มีรายมือชื่อของผู้เขียนหลักหรือผู้ที่ได้รับมอบอำนาจแทนผู้เขียนทุกนให้กับ JSSE ก่อนที่บทความจะมีการเผยแพร่ผ่านเว็บไซต์ของวารสาร
แบบโอนลิขสิทธิ์บทความ (Copyright Transfer Form)
ทางวารสาร JSSE ได้กำหนดให้มีการกรอกแบบโอนลิขสิทธิ์บทความให้ครบถ้วนและส่งมายังกองบรรณาธิการในข้อมูลเสริม (supplementary data) พร้อมกับนิพนธ์ต้นฉบับ (manuscript) ที่ส่งมาขอรับการตีพิมพ์ ทั้งนี้ ผู้เขียนหลัก (corresponding authors) หรือผู้รับมอบอำนาจ (ในฐานะตัวแทนของผู้เขียนทุกคน) สามารถดำเนินการโอนลิขสิทธิ์บทความแทนผู้เขียนทั้งหมดได้ ซึ่งสามารถอัพโหลดไฟล์บทความต้นฉบับ (Manuscript) และไฟล์แบบโอนลิขสิทธิ์บทความ (Copyright Transfer Form) ในเมนู “Upload Submission” ดังนี้
1. อัพโหลดไฟล์บทความต้นฉบับ (Manuscript) ในเมนูย่อย Article Component > Article Text
2. อัพโหลดไฟล์แบบโอนลิขสิทธิ์บทความ (Copyright Transfer Form) ในเมนูย่อย Article Component > Other
ดาวน์โหลด ไฟล์แบบโอนลิขสิทธิ์บทความ (Copyright Transfer Form)
เอกสารอ้างอิง
Hardman, N.R. and Jordan, J.H. (1967). A minimum problem connected with complete residue systems in Gaussian integers. The American Mathematical Monthly, 74(5), 559-561.
Jordan, J.H. and Potratz, C.J. (1965). Complete residue systems in the Gaussian integers. Mathematics Magazine, 38(1), 1-12.
Katai, I. and Szabo, J. (1975). Canonical number systems for complex integers. Acta Scientiarum Mathematicarum, 37, 255-260.
Pollard, H. and Diamond, H.G. (1975). The theory of algebraic numbers. New York: The Mathematical Association of America.
Tadee, S. (2021). Complete residue systems in the Gaussian integers (in Thai). Proceedings of 11st National Conference of Sri-Ayutthaya Rajabhat University Group (pp. 138-148). July 15, 2021. Chachoengsao: Rajabhat Rajanagarindra University.
Tadee, S., Laohakosol, V. and Damkaew, S. (2017). Explicit complete residue systems in a general quadratic field. Divulgaciones Matematicas, 18(2), 1-17.